四位全加器设计
什么是加法器
加法器是一种数字电路,用于执行二进制数的加法运算。它通常由多个全加器(Full Adder)组成,每个全加器负责处理两个二进制位以及进位输入,并产生一个和位以及一个进位输出。加法器在数字电路中广泛应用,是构成算术逻辑单元(ALU)的核心部件,广泛应用于计算机、数字信号处理器(DSP)以及各种需要进行算术运算的硬件系统中。
加法器的分类
根据处理的位数和进位处理方式,加法器可以分为半加器(Half Adder)和全加器(Full Adder)。
-
半加器:半加器将两个二进制位相加,并产生一个和位以及一个进位输出。半加器没有进位输入,因此只能处理最低位。
- 输入:两个单比特输入
A和B。 - 输出:一个和
S(Sum) 和一个进位C_out(Carry Out)。 - 逻辑:
S = A XOR B(异或门)C_out = A AND B(与门)
- 特点:只能计算两个单比特数之和,不考虑低位的进位输入
- 输入:两个单比特输入
-
全加器:全加器将三个二进制位相加,包括两个输入位和一个进位输入位,并产生一个和位以及一个进位输出。全加器可以处理多位加法,并且可以处理进位。
- 输入:三个单比特输入
A、B和一个来自低位的进位C_in(Carry In)。 - 输出:一个和
S和一个进位C_out。 - 逻辑:全加器可以由两个半加器和一个或门构成。
S = (A XOR B) XOR C_inC_out = (A AND B) OR (C_in AND (A XOR B))
- 特点:可以计算两个单比特数加上一个来自低位的进位,因此可以级联起来构建多比特加法器。
- 输入:三个单比特输入
-
一位全加器的Verilog实现
module fulladder(
input a,
input b,
input cin,
output sum,
output cout
);
//方法1:直接使用加法运算符
assign {cout,sum} = a + b + cin;
//方法2:使用半加器和全加器
assign sum = a ^ b ^ cin;
assign cout = (a & b) | (cin & (a ^ b));
//等价的标准形式(更对称)
//assign cout = (a & b) | (a & cin) | (b & cin);
endmodule两种方式对比:
- 可读性与抽象层次
| 方面 | 方法1 | 方法2 |
|---|---|---|
| 代码简洁性 | 非常简洁,一行代码 | 需要两行,稍复杂 |
| 设计意图 | 直观表达”加法”操作 | 表达底层逻辑关系 |
| 抽象层次 | 高层次(行为级) | 低层次(接近门级) |
方法1优势:设计意图清晰,一眼就能看出是在做加法运算。 方法2优势:对于学习数字逻辑、理解全加器原理更有帮助。
- 综合结果对比 现代综合工具(如Vivado、Quartus)对这两种写法通常会产生几乎相同的电路:
- 方法1 → 综合工具识别为加法器 → 优化后的门级电路
- 方法2 → 直接映射逻辑门 → 优化后的门级电路
- 可扩展性
方法1 在扩展到多位加法器时优势明显:
// 4位加法器 - 方法1写法
assign {cout, sum} = a + b + cin; // a, b, sum是4位方法2 扩展时需要显式实例化多个全加器并手动连接进位链。
多bit全加器
多比特加法器是用于处理多个二进制位加法运算的电路。它通常由多个全加器(Full Adder)级联构成,每个全加器负责处理相邻的二进制位以及进位输入,并产生一个和位以及一个进位输出。多比特加法器可以处理多位加法,并且可以处理进位。
- 输入:多个二进制位输入
A、B以及进位输入C_in。 - 输出:一个和
S和一个进位C_out。 - 逻辑:多比特加法器可以由多个全加器级联构成,每个全加器负责处理相邻的二进制位以及进位输入,并产生一个和位以及一个进位输出。
S = (A XOR B) XOR C_inC_out = (A AND B) OR (C_in AND (A XOR B))
- 特点:可以计算多个二进制位相加,并且可以处理进位。
串行进位加法器 (Ripple-Carry Adder)
-
基本概念
- 结构:将多个全加器串联起来,前一个全加器的
C_out连接到后一个全加器的C_in。 - 优点:结构简单,易于实现。
- 缺点:由于进位信号需要逐级传播,运算速度较慢,特别是对于位数较多的加法器,进位链的延迟会非常大,这被称为“进位传播延迟”。
- 结构:将多个全加器串联起来,前一个全加器的
-
进位传播延迟说明
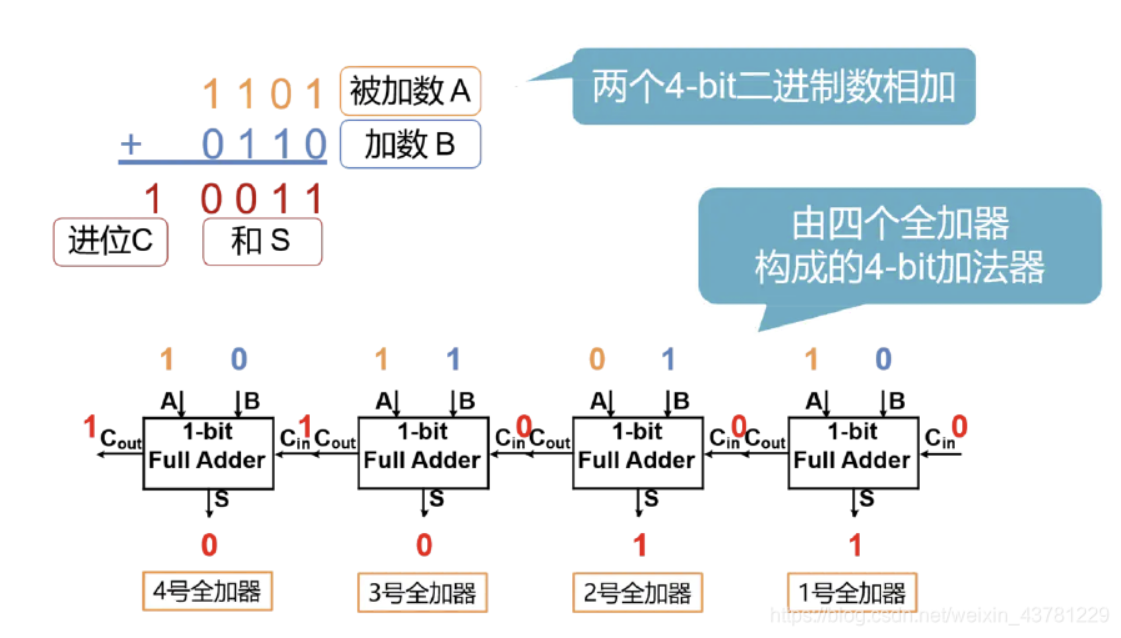
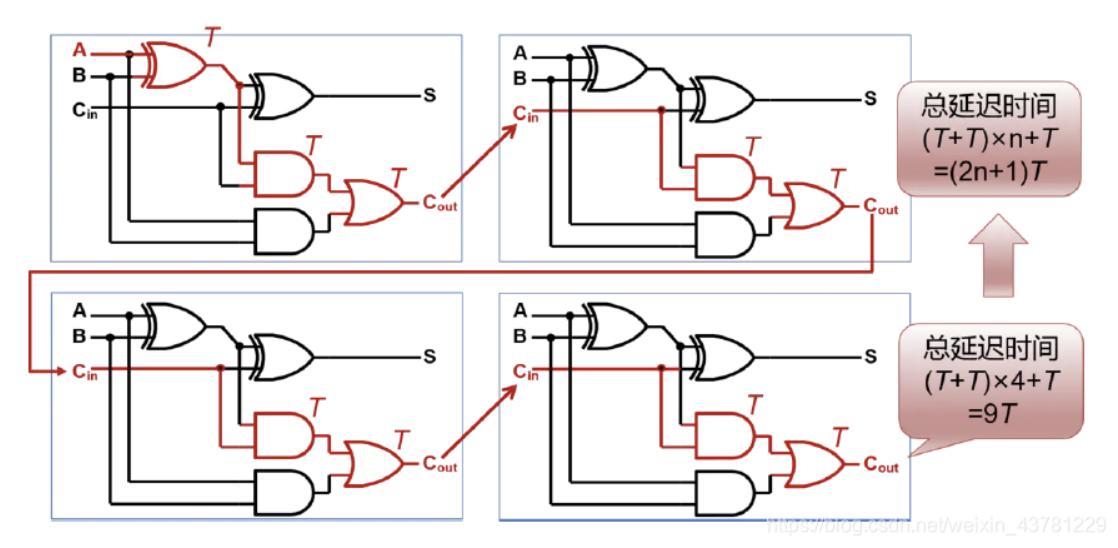
如果将上图全加器内部打开,可以看到,关键路上有9个门,门延迟非常高,如果位数较多,进位链的延迟会非常大,这被称为“进位传播延迟”。
超前进位加法器 (Carry-Lookahead Adder)
- 基本概念
- 结构:通过复杂的组合逻辑预先计算出所有位的进位,而不是等待低位进位传播。它使用“进位产生”(Generate)和“进位传播”(Propagate)概念。
- 优点:运算速度快,因为进位不再需要逐级传播。
- 缺点:硬件复杂,随着位数的增加,所需的门电路数量会显著增加。
- 原理说明 为了改进行波仅为加法器的延迟问题,可以将全加器的进位信号转化为有G和P以及本级进位输入组成的逻辑。如下图所示:

将四个加法器串联,迭代可以得到
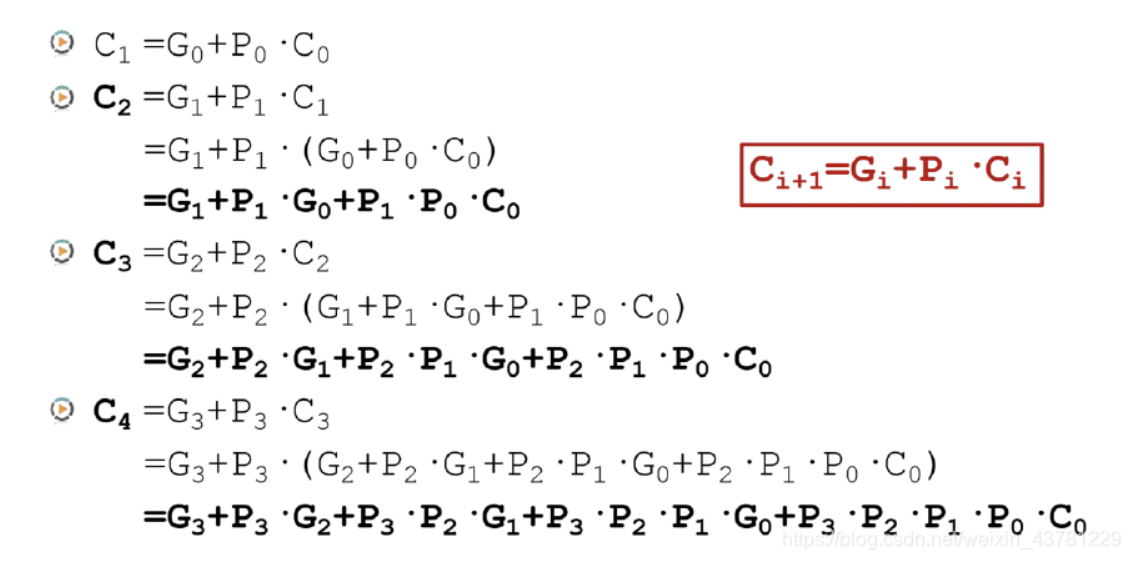
可以看到,每一级的进位都不依赖于上一级的进位,因此不需要等待上一个加法器完成计算,超前得到进位结果。同时,显然如果要实现大位宽加法器,逻辑将会变得更加复杂。
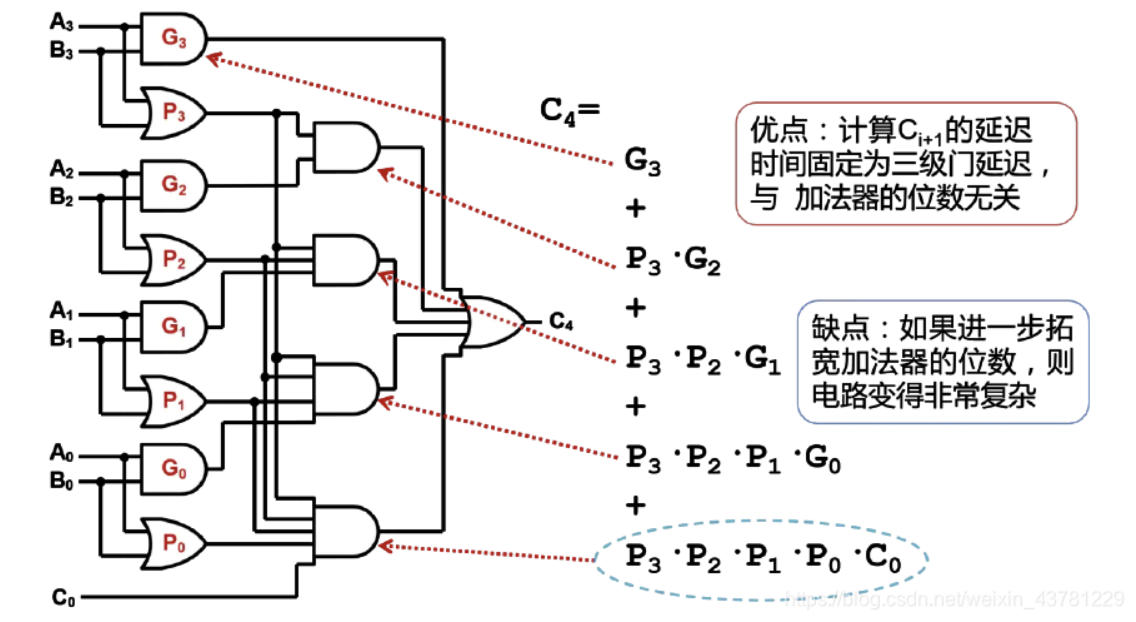
通过超前进位的方法,实现四位全加器的原理图如下
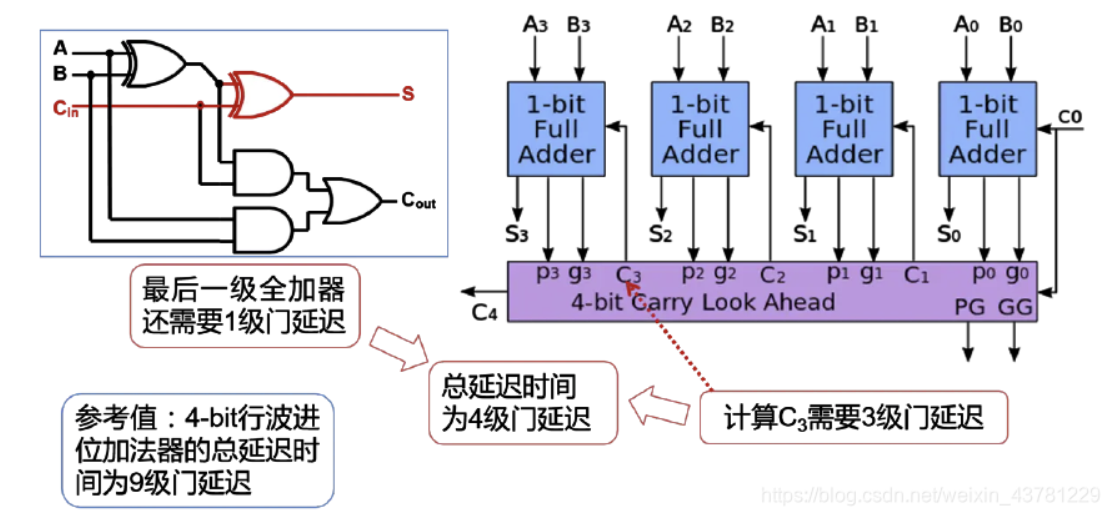
四位全加器设计
四位全加器可以由四个全加器组成,每个全加器负责处理两个二进制位以及进位输入,并产生一个和位以及一个进位输出。四位全加器可以处理四位二进制数的加法运算,并且可以处理进位。
四位串行进位全加器的Verilog实现
模块框图
接口定义
| 信号 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| clk | input | 1 | 时钟信号 |
| rst_n | input | 1 | 复位信号,低电平有效 |
| a | input | 4 | 加数A |
| b | input | 4 | 加数B |
| cin | input | 1 | 进位输入 |
| sum | output | 4 | 和 |
| cout | output | 1 | 进位输出 |
接口时序
模块实现
module addr4(
input clk ,
input rst_n ,
input [3:0] a ,
input [3:0] b ,
input cin ,
output sum ,
output cout
);
assign {cout,sum} = a + b + cin;
endmodule